鳳・テブナンの定理

公式　鳳・テブナンの定理

今日はノートに

と書きましょう。

鳳・テブナンの定理とは

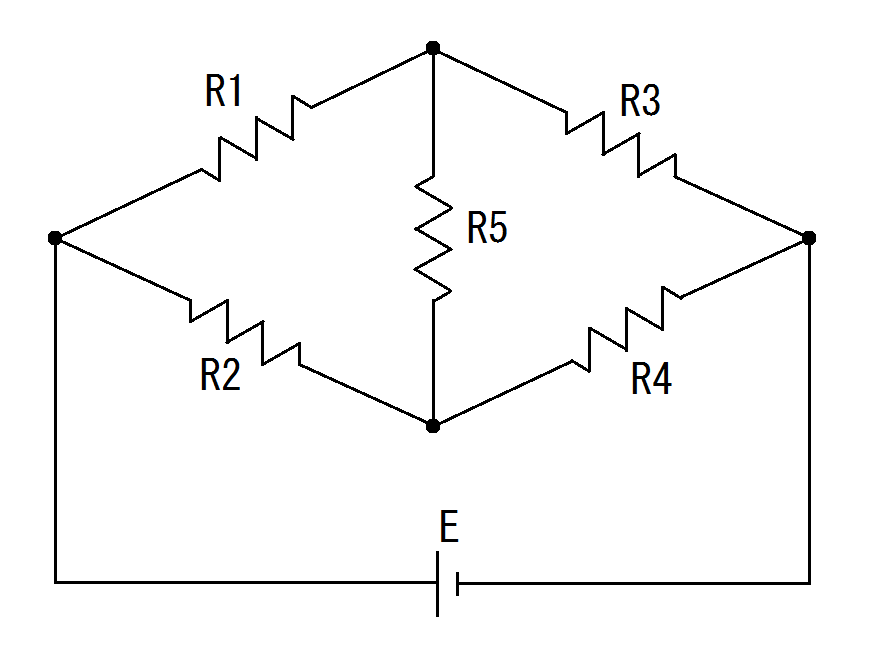
図1. ブリッジ回路例

図1.のような複雑な回路は

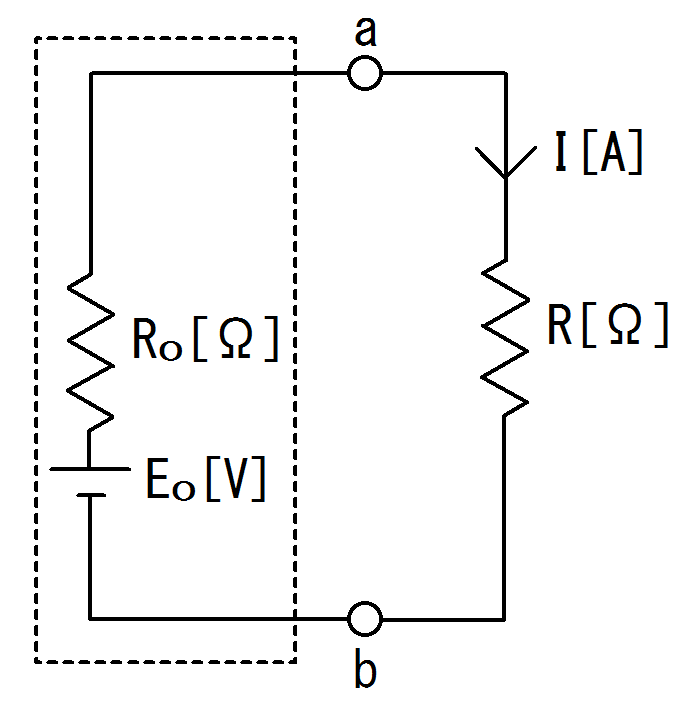
図2. 図1.の等価回路図

図2.のような、目的の抵抗とそれ以外の合成抵抗として考えることができます。

これが鳳・テブナンの定理になります。

こうすれば抵抗2本の直列回路なので電圧や電流を簡単に求めることできます。

ちなみに、合成抵抗を求める際には電圧源は短絡して、電流源は開放して求めます。

大丈夫です。この定理びっくりするぐらい「ブリッジ回路」にしか出てこないです。

ブリッジ回路でない場合でも次の例題から使い方をマスターしてもらえれば使い方はバッチリでしょう。

例題　ブリッジ回路

図3.のようなブリッジ回路がある。

抵抗$R_{1}=3[Ω]、R_{2}=12[Ω]、R_{3}=6[Ω]、R_{4}=4[Ω]、R_{5}=5[Ω]$である。

電源電圧$E=24[V]$のとき、抵抗$R_{5}$に流れる電流$I_{5}[A]$はいくつか。

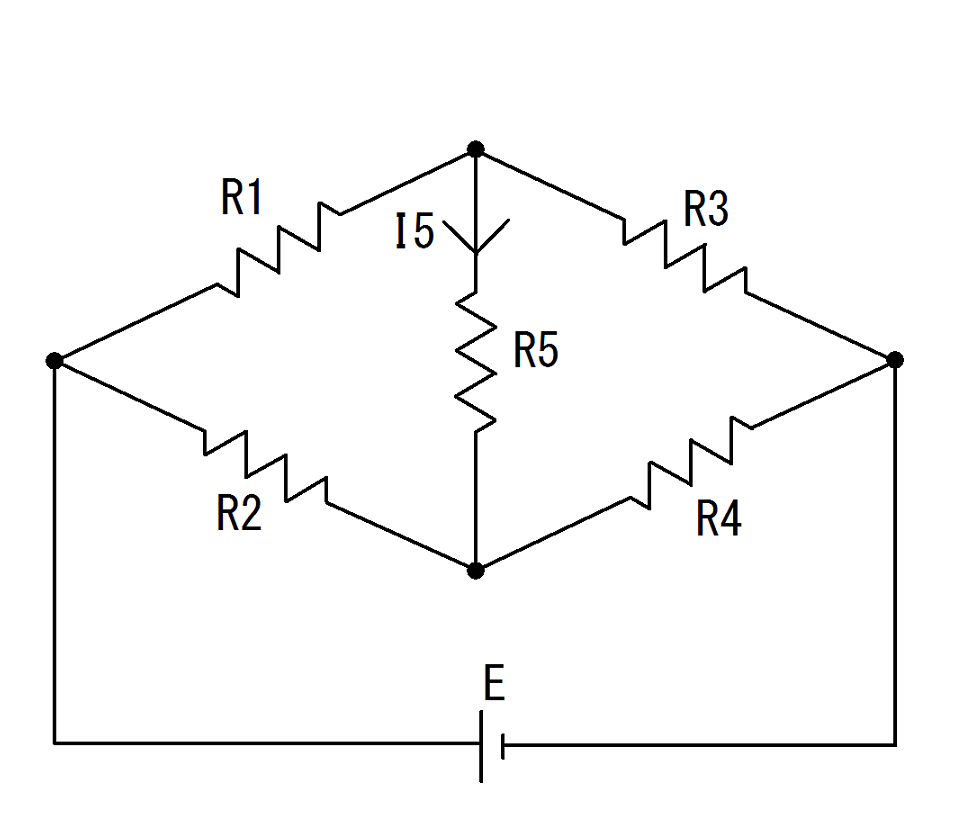
図3. ブリッジ回路

STEP1　等価回路図を描いてみる

まず、抵抗$R_{5}$を取り出します。

図で書き直すと図4.の通りです。

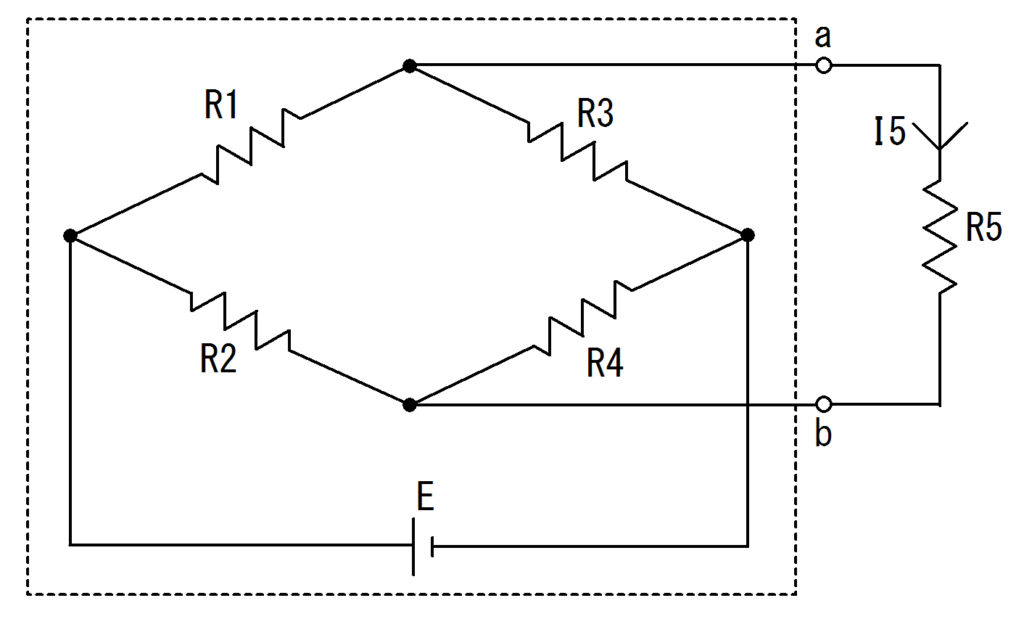
図4. 図3.の等価回路

点線で囲われた部分の電圧$E_{0}$と抵抗$R_{0}$を求めれば抵抗$R_{5}$との直列回路だけになり、簡単に電流$I_{5}$が求まります。

STEP2　電圧$E_{0}$を求める

電圧$E_{0}$はa-b間の電圧になります。

a-b間の電圧を求めるには、まずa-b間を開放します。

図で表すと図5.通りです。

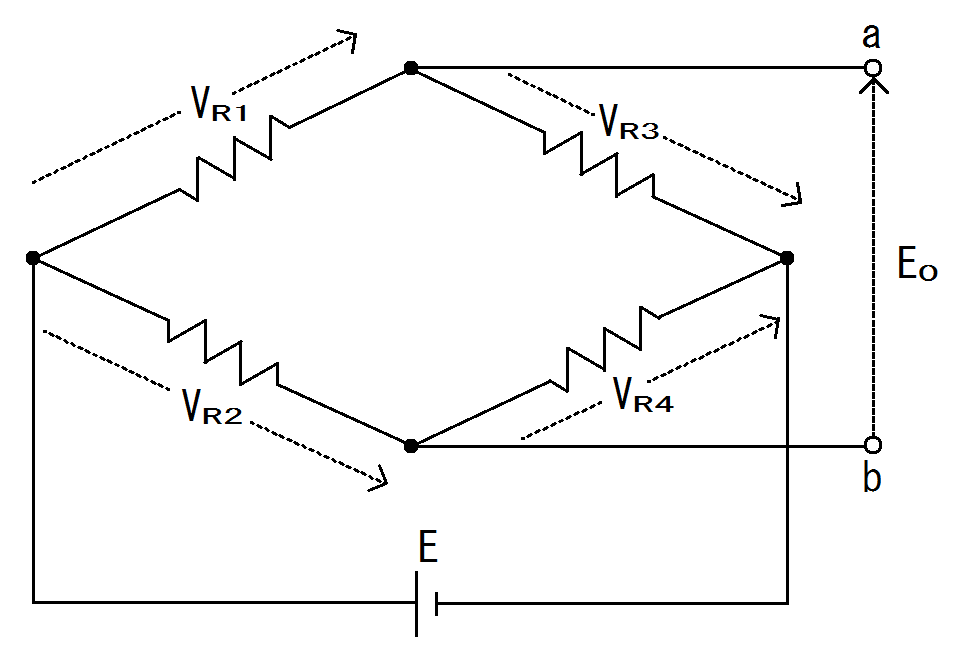
図5. 鳳・テブナンの定理を用いて電圧$E_{0}$を求める図

そして電圧$E_{0}$は$E_{0}=V_{R2}-V_{R1}=V_{R3}-V_{R4}$で求まります。

aからbまでの電圧は$V_{R1}$は逆方向、$V_{R2}$は順方向、$V_{R3}$も順方向、$V_{R4}$は逆方向なので上のような式になります。

$V_{R1}=E\dfrac{R1}{R1+R3}=24×\dfrac{3}{3+6}=8[V]$

$V_{R2}=E\dfrac{R2}{R2+R4}=24×\dfrac{12}{12+4}=18[V]$

$E_{0}=V_{R2}-V_{R1}=18-8=10[V]$になります。

STEP3　電圧$R_{0}$を求める

合成抵抗を求める際には電圧源は短絡して、電流源は開放して求めます。

電圧源がありますので、そこを短絡すると図6.のようになります。

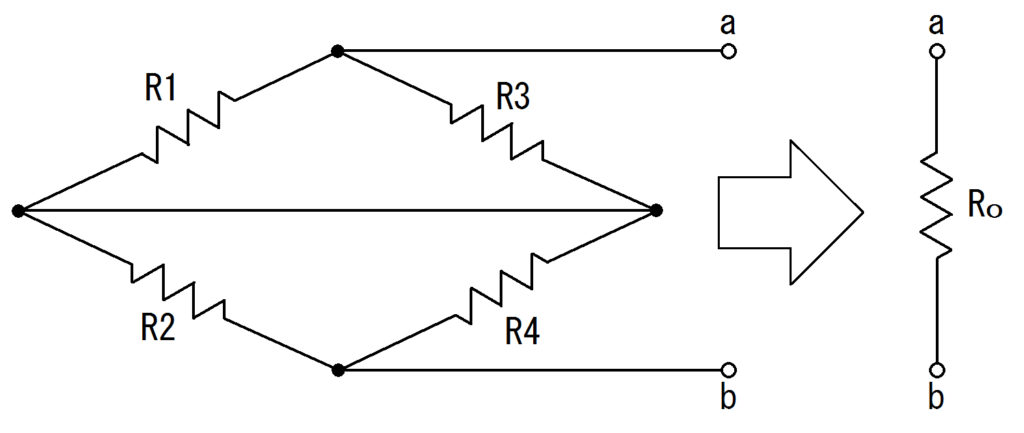
図6. 鳳・テブナンの定理を用いて抵抗$R_{0}$を求める図

つまり、抵抗$R1$と抵抗$R3$が並列に、抵抗$R2$と抵抗$R4$も並列に、それが直列に繋がった回路が抵抗$R_{o}$になります。

抵抗$R1$と抵抗$R3$の並列合成抵抗　$\dfrac{R1R3}{R1+R3}=\dfrac{3×6}{3+6}=\dfrac{18}{9}=2[Ω]$

抵抗$R2$と抵抗$R4$の並列合成抵抗　$\dfrac{R2R4}{R2+R4}=\dfrac{12×4}{12+4}=\dfrac{48}{16}=3[Ω]$

抵抗$R_{o}=2+3=5[Ω]$

STEP4　電流$I5$を求める

あとは抵抗$R5$との直列回路なのでオームの法則で求まります。

電流$I5=\dfrac{E_{0}}{R_{0}+R5}=\dfrac{10}{5+5}=1[A]$

鳳・テブナンの定理はこのように使います。

今回は、式よりも使い方を覚えることが重要になります。

公式を見て使い方を思い出せるようになれば、鳳・テブナンの定理は完璧です。