キルヒホッフの法則

公式　キルヒホッフの法則

今日はノートに

と書きましょう。

キルヒホッフの法則とは

キルヒホッフの第一法則

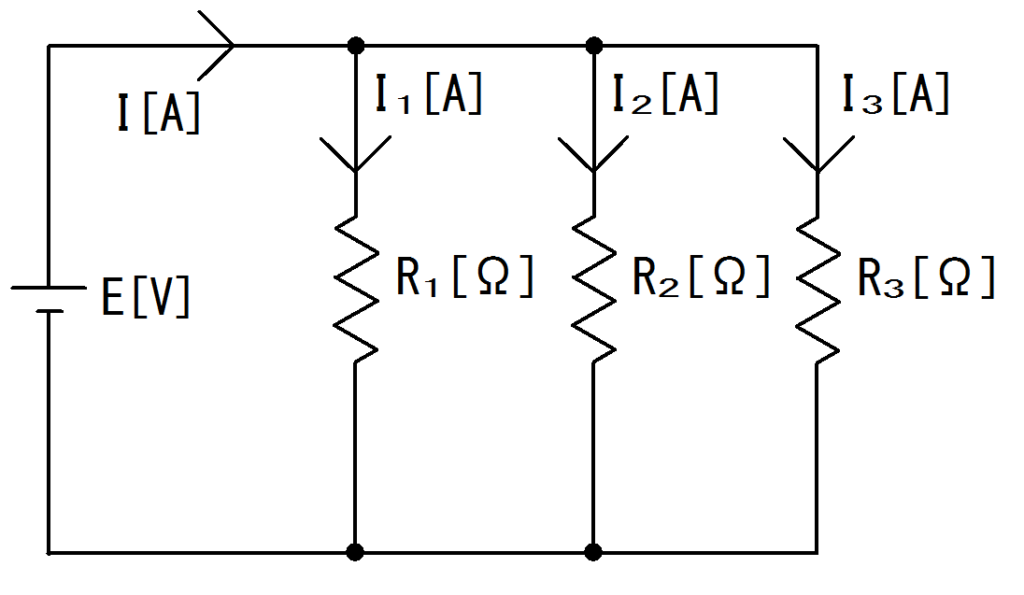
図1. 3並列回路図

キルヒホッフの第一法則は、流入する電流の和と流出する電流の和は等しいというものです。

図1.の場合、流入する電流（分かれる前）は$I$で、流出する電流（分かれた後）は$I_{1}$と$I_{2}$と$I_{3}$になります。

これを式で表すと$I=I_{1}+I_{2}+I_{3}[A]$となります。

キルヒホッフの第二法則

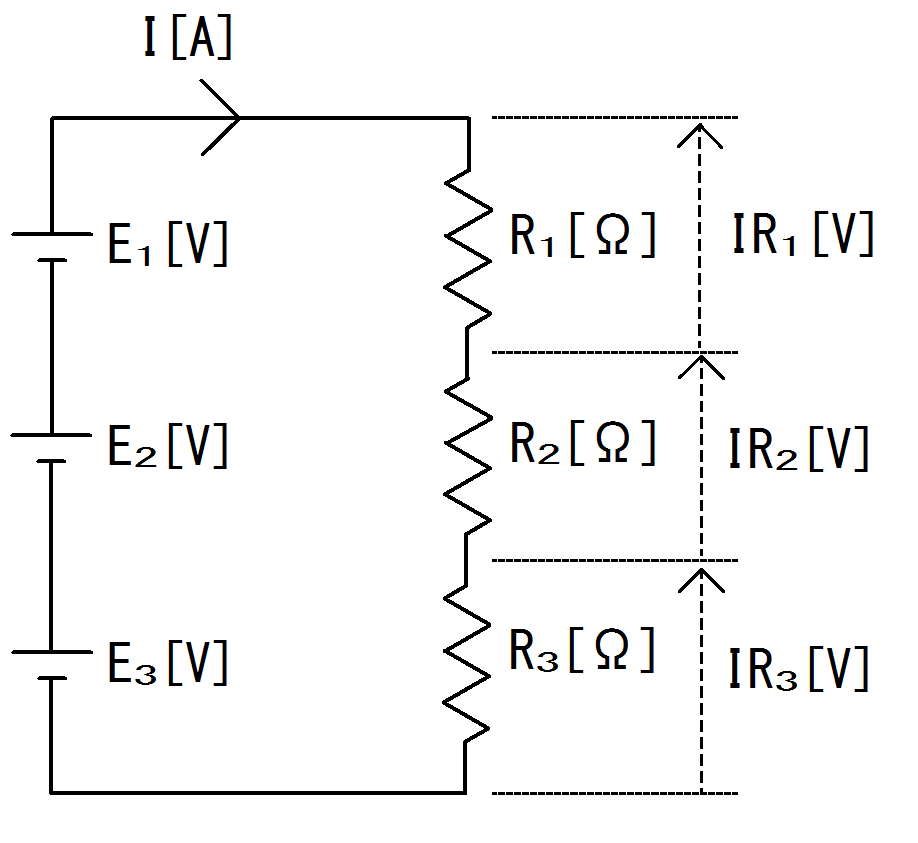
図2. 3直列回路図

キルヒホッフの第二法則は、起電力の和と電圧降下の和は等しいというものです。

図2.の場合、起電力（電源）は$E_{1}$と$E_{2}$と$E_{3}$で、電圧降下（抵抗端の電位差）は$IR_{1}$と$IR_{2}$と$IR_{3}$になります。

例題　複数の電源を持つ回路

図3.のような回路がある。

抵抗$R_{1}=R_{2}=R_{3}=2[Ω]$である。

電源電圧$E_{1}=15[V]、E_{2}=10[V]、E_{3}=5[V]$のとき、

抵抗$R_{1}$に流れる電流$I_{1}[A]$はいくつか。

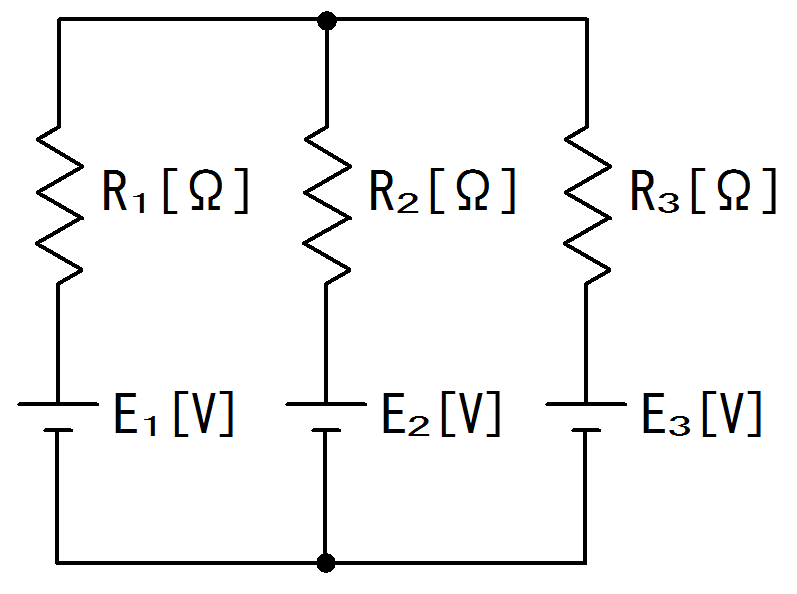
図3. 複数の電源を持つ回路図

キルヒホッフの第一法則より式$a$を$I_{1}+I_{2}=I_{3}$とする。

キルヒホッフの第二法則より式①を$E_{1}-E_{3}=I_{1}R_{1}+I_{3}R_{3}$として、

式②を$E_{2}-E_{3}=I_{2}R_{2}+I_{3}R_{3}$とする。

図で表すと図4.のようになります。

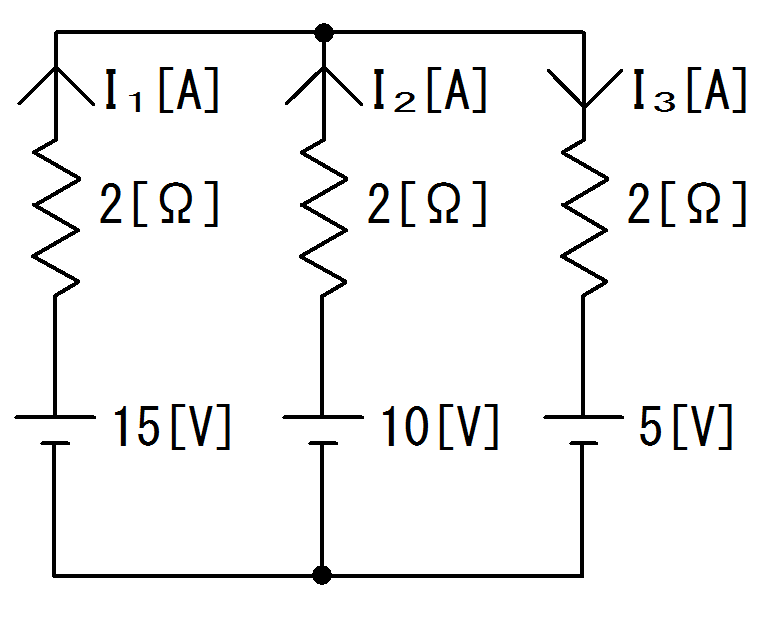
図4. 図3.の電流経路図

キルヒホッフの第二法則で立てた式①と式②にキルヒホッフの第一法則で立てた式$a$を代入します。

式①に式$a$を代入　$E_{1}-E_{3}=I_{1}R_{1}+I_{1}R_{3}+I_{2}R_{3}$・・・①’

式②に式$a$を代入　$E_{2}-E_{3}=I_{2}R_{2}+I_{1}R_{3}+I_{2}R_{3}$・・・②’

与えられた抵抗値・電圧値を代入します。

①’に数値を代入　$15-5=2I_{1}+2I_{1}+2I_{2}$　　　$10=4I_{1}+2I_{2}$

②’に数値を代入　$10-5=2I_{2}+2I_{1}+2I_{2}$　　　$5=2I_{1}+4I_{2}$

式①’×2－式②’より$I_{1}[A]$を求めます。

式①’×2　$20=8I_{1}+4I_{2}$

式①’×2－式②’　$20-5=8I_{1}+4I_{2}-2I_{1}-4I_{2}$　　　$15=6I_{1}$

$I_{1}=2.5[A]$となります。

ちなみに残りの$I_{2}$および$I_{3}$についても代入して求めことができます。

代入すると$I_{2}=0[A]$、$I_{3}=2.5[A]$と求まります。

キルヒホッフの法則については以上になりますが、少し補足をします。

直流回路では例題のように、電圧のプラス極がどちらでマイナス極がどちらであるか、どこからどこに向かって電流が流れるか、電圧がどちらの極性であるかを見極めることが問題を解くコツになります。

直流回路では極性に気を付けて問題を解いてみてください。