直列回路・並列回路

公式　直列回路・並列回路

今日はノートに

と書きましょう。

直列回路・並列回路の公式の使い方

直列回路の場合

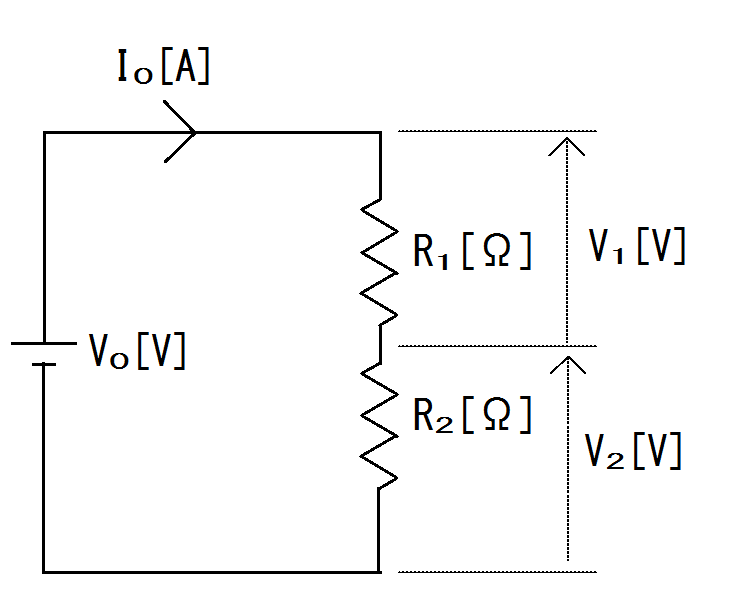
図1. 直列回路図

図1.のように抵抗が直列接続された場合は、2つの抵抗を1つの合成抵抗として扱うことができる。

直列回路では合成抵抗$R_{0}$は$R_{0}=R_{1}+R_{2}$となる。

抵抗$R_{1}$と$R_{2}$に加わる電圧$V_{1}$と$V_{2}$、

$V_{1}=V_{0}\dfrac{R_{1}}{R_{1}+R_{2}}[V]$

$V_{2}=V_{0}\dfrac{R_{2}}{R_{1}+R_{2}}[V]$と比例分配されます。

電源電圧$V_{0}$で表す場合では、$V_{0}=V_{1}+V_{2}[V]$となります。

また直流回路の電流は、$I_{0}=I_{1}=I_{2}[A]$と全て同じになります。

並列回路の場合

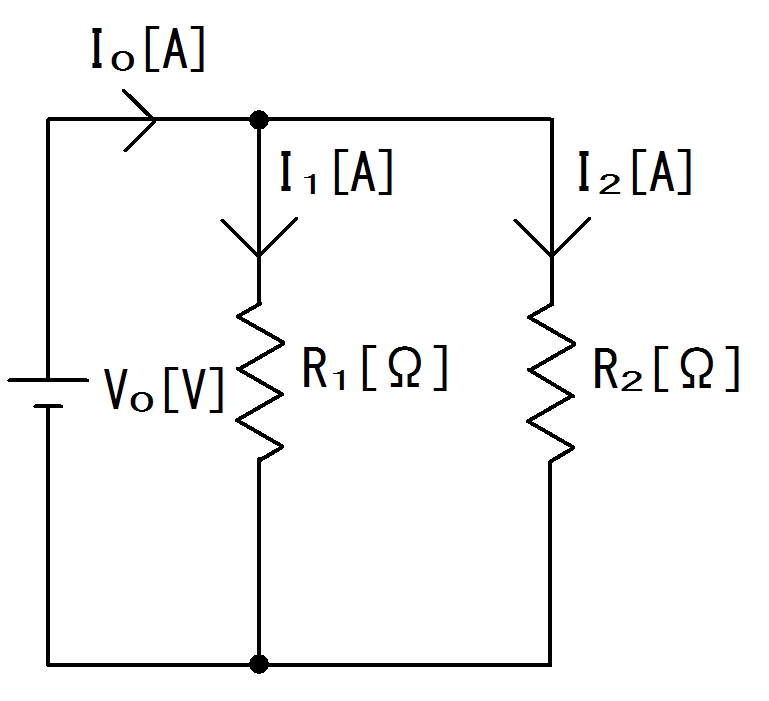
図2. 並列回路図

図2.のように抵抗が並列接続された場合も、2つの抵抗を1つの合成抵抗として扱うことができる。

並列回路では合成抵抗$R_{0}$は$R_{0}=\dfrac{R_{1}R_{2}}{R_{1}+R_{2}}[Ω]$となる。

抵抗$R_{1}$と$R_{2}$に流れる電流は、

$I_{1}=I_{0}\dfrac{R_{2}}{R_{1}+R_{2}}[A]$

$I_{2}=I_{0}\dfrac{R_{1}}{R_{1}+R_{2}}[A]$となります。

電源電流$I_{0}$で表す場合では、$I_{0}=I_{1}+I_{2}[A]$となります。

また並列回路では逆に電圧が、$V_{0}=V_{1}=V_{2}[V]$と全て同じになります。

ちなみに抵抗が3つの場合の直列回路と並列回路では以下の通りです。

直列回路　$R_{0}=R_{1}+R_{2}+R_{3}[Ω]$

　　　　　　$V_{1}=V_{0}\dfrac{R_{1}}{R_{1}+R_{2}+R_{3}}[V]$

　　　　　　$I_{0}=I_{1}=I_{2}=I_{3}[A]$

並列回路　$R_{0}=\dfrac{R_{1}R_{2}R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}[Ω]$

　　　　　($\dfrac{1}{R_{0}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}[Ω]$)

　　　　　　$I_{1}=I_{0}\dfrac{R_{2}R_{3}}{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}[A]$　　　　　　

　　　　　　$V_{0}=V_{1}=V_{2}=V_{3}[V]$

個人的には並列回路の抵抗が増えた場合、覚えやすさを優先して

$\dfrac{1}{R_{0}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}[Ω]$で覚えています。

どちらでもよいですが、まずは覚えること重要ですので覚えやすい方を選びましょう。

例題　直並列回路

図3.のような回路がある。

抵抗は$R_{1}=2.5[Ω]、R_{2}=30[Ω]、R_{3}=10[Ω]$であり、

抵抗$R_{2}$に流れる電流$I_{2}=0.5[A]$であった。

電源電圧$E[V]$はいくつか。

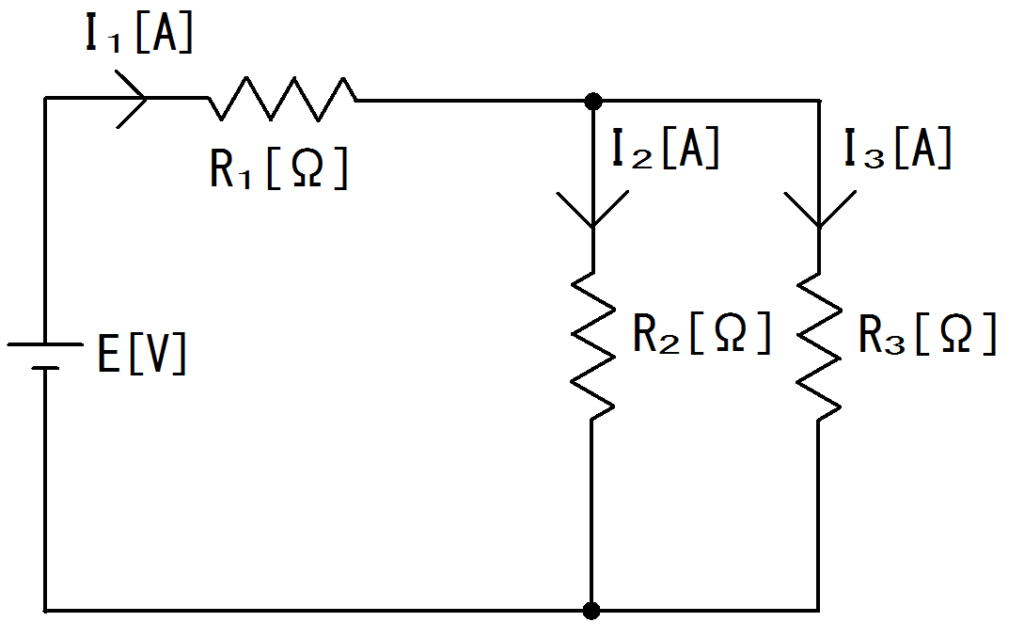
図3. 直並列回路図

抵抗$R_{2}$に加わる電圧$V_{2}$は

$V_{2}=I_{2}R_{2}=0.5[A]×30[Ω]=15[V]$

並列回路なので抵抗$R_{3}$に加わる電圧$V_{3}$は

$V_{3}=V_{2}=15[V]$

抵抗$R_{3}$に流れる電流$I_{3}$は

$I_{3}=\dfrac{V_{3}}{R_{3}}=\dfrac{15[V]}{10[Ω]}=1.5[A]$

電源電流、つまりここでの電流$I_{1}$は

$I_{1}=I_{2}+I_{3}=0.5[A]+1.5[A]=2.0[A]$となります。

抵抗$R_{1}$に加わる電圧$V_{1}$は

$V_{1}=I_{1}R_{1}=2.0[A]×2.5[Ω]=5[V]$

直列回路なので電源電圧$E$は

$E=V_{1}+V_{2}=V_{1}+V_{3}=5[V]+15[V]=20[V]$となります。

このように1つ1つ値を求めていけば解けますので、わかるところから埋めていきましょう。

直列回路・並列回路については以上になります。