公式 帆足・ミルマンの定理

ほあし・ミルマンって読むのかな?

ほあし・ミルマンの定理で合ってます。
今日はノートに
$V_{ab}=\dfrac{\dfrac{E_{1}}{R_{1}}+\dfrac{E_{2}}{R_{2}}+\dfrac{E_{3}}{R_{3}}}{\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}}[V]$
と書きましょう。
帆足・ミルマンの定理とは
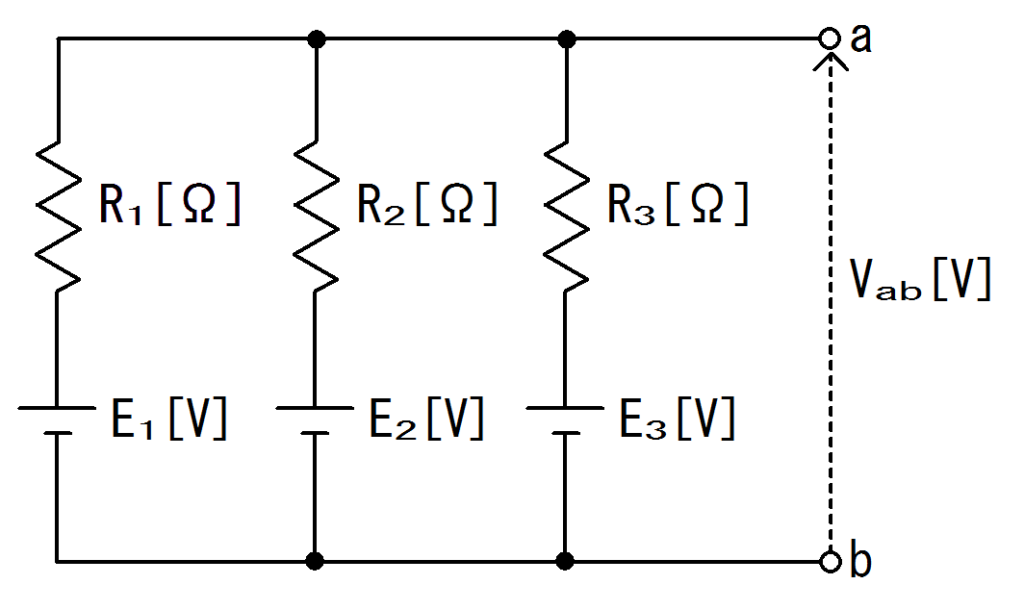
図1. 電源と抵抗の並列群回路図
図1.のように、電源と抵抗が複数並列になっているときに使う公式です。
そして、電圧$V_{ab}$を求めることができると、そこに電源があると仮定して回路を組みことができそれぞれの抵抗$R_{1}、R_{2}、R_{3}$に流れる電流を求めることができます。

この公式の細かい使い方も以下の例題で説明します。
例題 並列回路群
図2.のような回路がある。
それぞれ抵抗は$R_{1}=6[Ω]、R_{2}=3[Ω]、R_{3}=2[Ω]$である。
電源電圧$E_{1}=24[V]、E_{2}=9[V]、E_{3}=2[V]$のとき、
抵抗$R_{1}$に流れる電流$I_{1}$はいくつか。
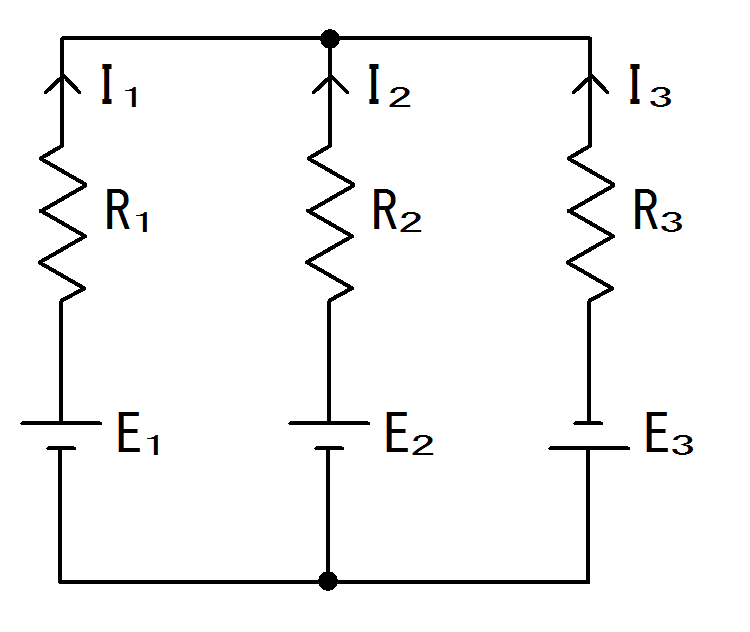
図2. 並列群回路図

繰り返しになりますが、まず直流回路なので極性に注意します。
帆足・ミルマンの定理より、公式に値を入れて回路の端子電圧$V_{ab}$を求めます。
$V_{ab}=\dfrac{\dfrac{E_{1}}{R_{1}}+\dfrac{E_{2}}{R_{2}}+\dfrac{E_{3}}{R_{3}}}{\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}}=\dfrac{\dfrac{24}{6}+\dfrac{9}{3}-\dfrac{2}{2}}{\dfrac{1}{6}+\dfrac{1}{3}+\dfrac{1}{2}}=4+3-1=6[V]$
次に電源電圧$E_{1}$から端子電圧$V_{ab}$を流れる電流$I_{1}$を求めます。
回路にすると図3.のようになります。
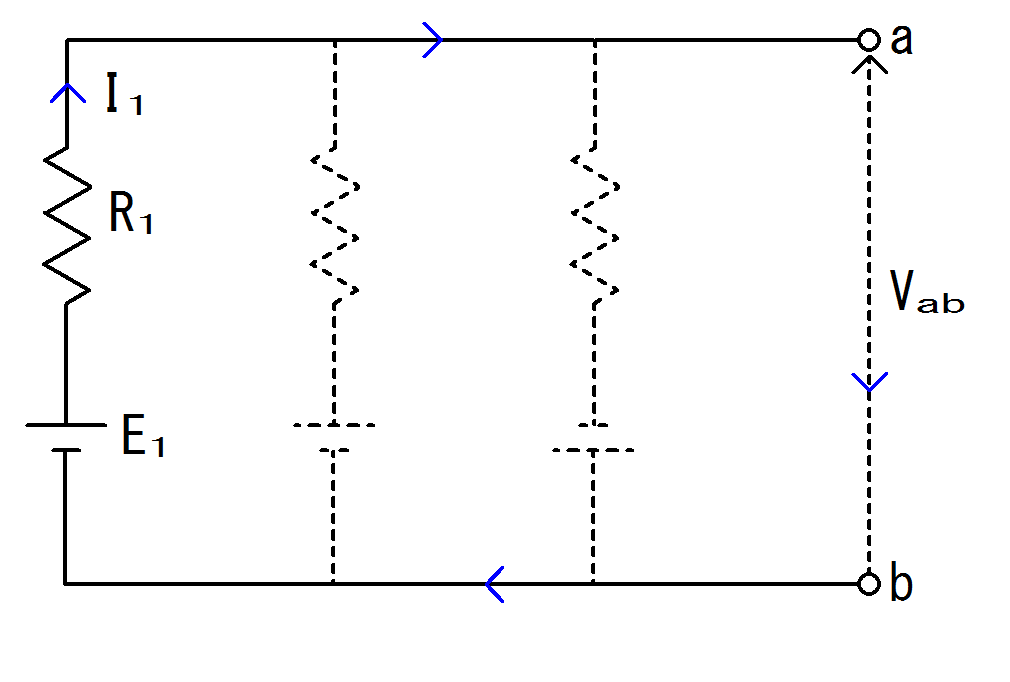
図3.電源$E_{1}$のみの回路図

へぇー、電源電圧$E_{2}$や$E_{3}$は無視できるのか。
回路は一周すれば成り立つので、問題ありません。
電流$I_{1}=\dfrac{E_{1}-V_{ab}}{R_{1}}=\dfrac{24-6}{6}=3[A]$と求まります。
他の電流$I_{2}$や$I_{3}$も同様に
$I_{2}=1[A]$、$I_{3}=-4[A]$
と求まります。

そもそもこの問題、見覚えがあるけど・・・。

キルヒホッフの法則でやった例題にとても似ています。
あれも、この公式を使って解くことができます。
帆足・ミルマンの定理や前回の鳳・テブナンの定理は、厳密には覚えなくてもキルヒホッフの法則で解くことができます。
しかし、キルヒホッフの法則で解くととても時間がかかるため、覚えておきましょう。
今日は以上になります。
お疲れ様でした。






コメント